Suponga que usted está en un colegio. En un patio se han congregado todos los alumnos (y alumnas). Lo curioso es que hay exactamente la misma cantidad de mujeres que de varones. Uno de los profesores de Educación Física toma el micrófono y les dice:
“Distribúyanse en el patio (que es muy grande) de manera tal de seguir la siguiente regla: entre dos varones tiene que haber ubicada una nena pero también al revés: entre dos nenas tiene que haber un nene.
“Para ser más explícito: si yo elijo dos nenas cualesquiera, en el segmento que las une tiene que haber un nene, pero si yo elijo dos nenes cualesquiera, en el segmento que los une tiene que haber una mujer.
“Yo me voy a dar vuelta y cuando ustedes me avisen que ya lo lograron, yo, sin mirar, les voy a decir cuál fue la distribución que encontraron”
Preguntas
¿Cuántas distribuciones posibles hay? ¿Cuál o cuáles pudieron haber encontrado los alumnos? ¿Cómo podía saber el profesor sin mirar? Fíjese lo que le parece: tome un papel y una lapicera e intente usted. Verá lo que sucede. Yo sigo acá abajo.
Solución
Espero que usted lo haya intentado porque así entenderá lo que voy a escribir acá abajo. Cuando uno quiere encontrar una distribución de todos los alumnos, descubre que hay una única forma: ¡ponerlos a todos en hilera, alternando hombres y mujeres!
Seguro que esta es una potencial distribución que cumple con la regla que pidió el profesor, pero la pregunta que subsiste es: ¿Es la única? Y si fuera la única, ¿Por qué?
En principio, me quiero quedar tranquilo en que usted puede visualizar que poner a todos en una fila alternando los sexos es efectivamente una solución. Lo que me parece interesante es mostrar que no puede haber ninguna otra forma. Veamos.
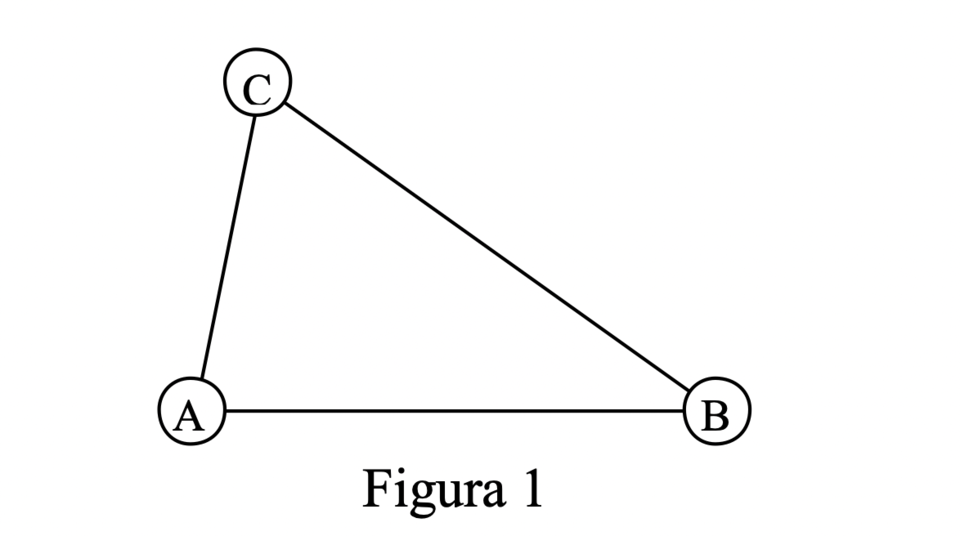
Supongamos que sí. Supongamos que hubiera alguna otra forma de distribuirlos cumpliendo la regla pedida de manera tal que no todos estén ubicados en una fila. Por lo tanto, en esta nueva forma, quedarán formados algunos triángulos, en donde los vértices son tres estudiantes cualesquiera. Es muy posible incluso que haya muchos de estos triángulos. Si así fuere, de todos los triángulos que hay, elijo el que tenga el área o la superficie más chica. Es decir, como habrá un número finito de triángulos, tiene que haber alguno que tenga el menor área entre todos. Si hubiera dos (o más) de área mínima, elijo uno cualquiera de ellos y lo llamo ABC (fíjese en la Figura 1).
Seguro que dos de los tres vértices tienen que ser estudiantes del mismo sexo, quizás los tres, pero lo que importa es que hay por lo menos dos que son varones o dos mujeres.
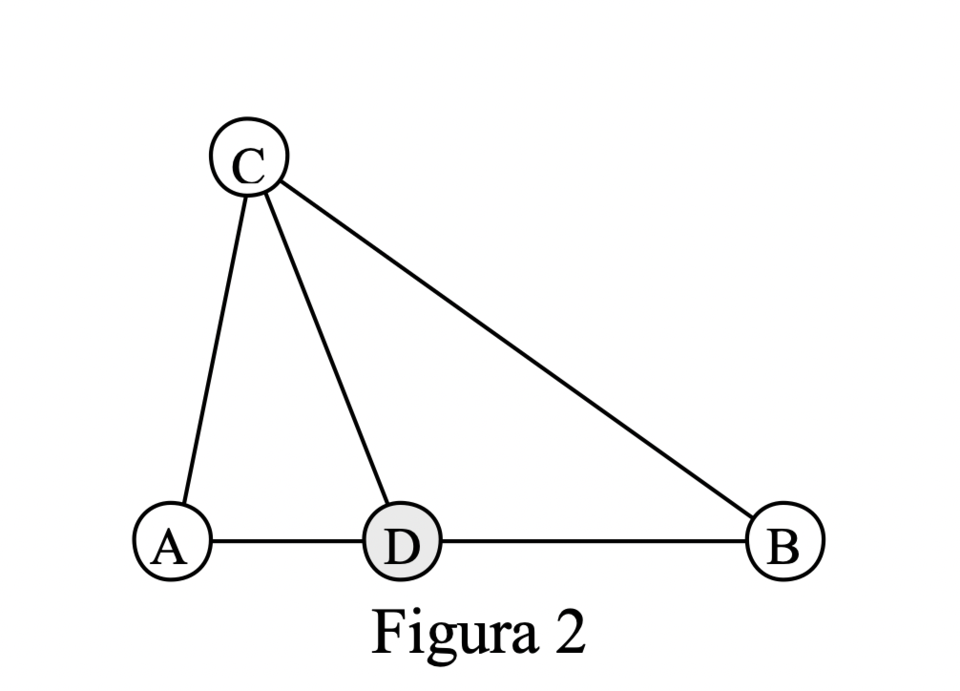
Como dos de ellos tienen que ser del mismo sexo, supongamos que A y B son dos varones. Siguiendo la regla, tiene que haber una niña que esté entre A y B. La voy a llamar D (como se ve en la Figura 2)
¿Qué le sugiere esta figura? Piense que si tiene que haber una niña (D), entonces hay otros dos triángulos que quedaron formados: ACD y DCB. Si recuerda, el triángulo ABC lo elegimos porque era de todos los posibles triángulos el que tenía menor área. Sin embargo, cualquiera de los dos ‘nuevos’ tiene área menor ¿Moraleja? Haber creído que existía un triángulo siquiera, fue lo que nos llevó a una contradicción. Por lo tanto, ¡no hay triángulos! Y si no hay triángulos, es porque están todos en una misma fila (o hilera). ¡Y listo!
El profesor sabía lo que habría de encontrar, mucho antes de darse vuelta, y por supuesto, no necesitaba mirar nada. El razonamiento matemático (sencillo) le permitió decidir cuál sería la solución (todos en una hilera) porque cualquier otra potencial distribución hubiera implicado la existencia de triángulos, y como escribí más arriba, si se pudiera forma alguno, eso contradiría la regla planteada originalmente ¿No le resulta bonita esta demostración?
![function body_3(chk,ctx){return chk.f(ctx.getPath(false, ["author","title"]),ctx,"h");}](https://images.pagina12.com.ar/styles/width470/public/2016-10/Adri%C3%A0n-Paenza.png?itok=t4lkwVR2)