¿Hay más números naturales que números pares? Supongamos que hay un cine en el que iban a pasar en tres dimensiones el partido final del campeonato del mundo. El dueño del teatro decidió que no cobraría la entrada, pero por una disposición municipal, cada persona necesitaba tener una entrada, para evitar que hubiera gente parada. Llegado este punto, la pregunta es: ¿cómo puede hacer usted para saber si tendrá lugar o no? 

Por supuesto, hay múltiples maneras de encontrar la respuesta. Una forma sería quedarse en la cola esperando que a uno le llegue el turno. Si todavía queda/n entrada/s, listo. Podría pasar también, que las localidades se agotaran antes que le toque a usted. En este caso, usted también sabría que no hay lugar antes de llegar hasta la puerta. Otra idea podría ser preguntar cuántas butacas tiene el cine y después, contar el número de personas que hay en la cola. 

Si no fuera necesario tener un ticket o si no hubiera problemas en que haya gente parada, uno podría dejarlos pasar a todos de manera tal que cada uno se ubique en algún asiento. Si se acaban las sillas antes que termine de entrar el público, es porque había más personas que butacas. Si la cola se agota y todavía quedan asientos libres, es porque había menos personas que lugares. Y si al terminar de entrar todos, no queda ningún asiento vacío ni hay ninguna persona parada, es porque hay exactamente el mismo número de personas que de butacas. En este último caso, no hace falta contar nada: no hace falta saber cuántas butacas hay en el cine ni contar cuántas personas hay en la cola. Basta con que cada uno ocupe un asiento y listo. 

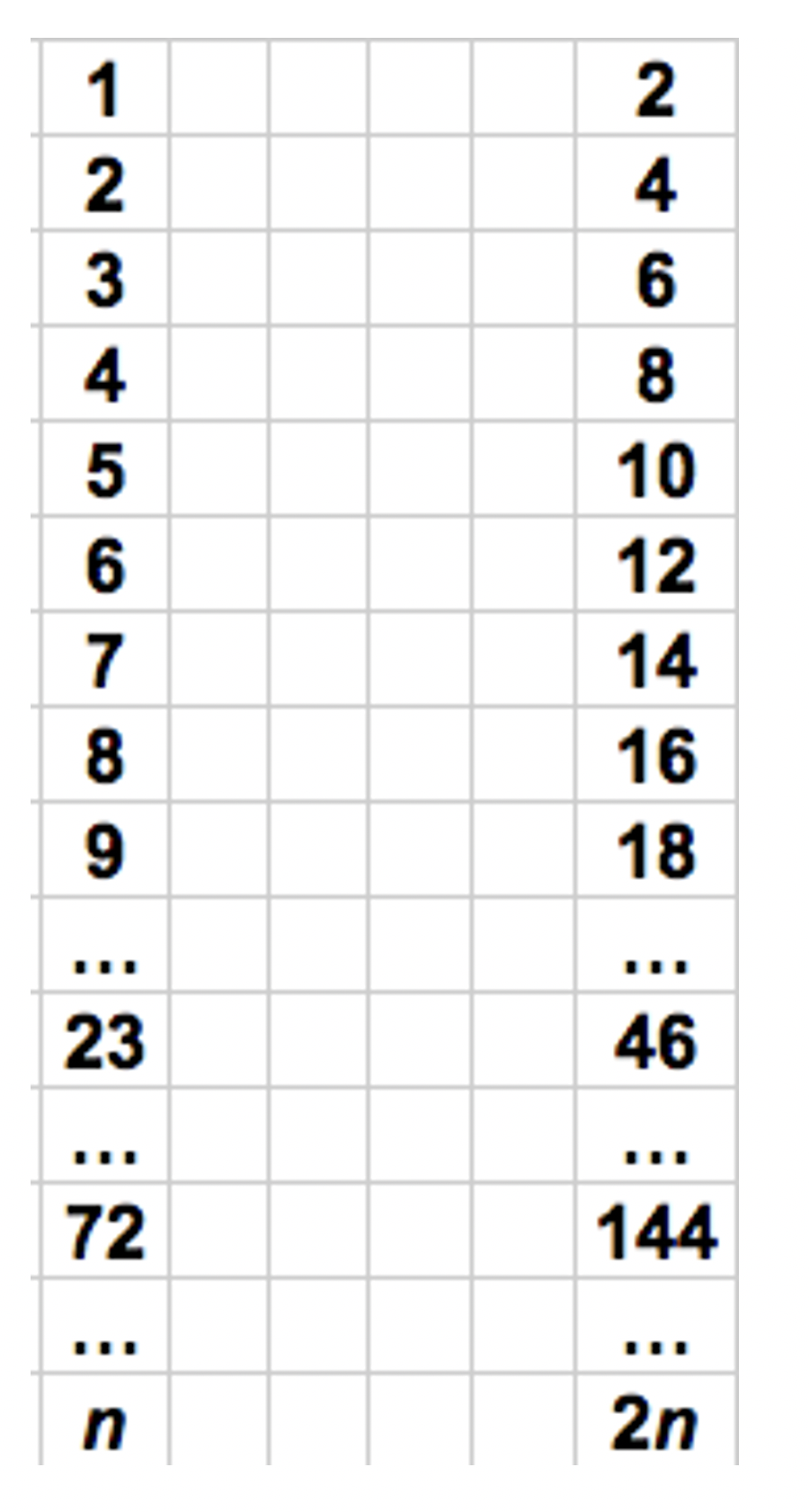
Siguiendo esta misma idea, quiero proponerle que pensemos si hay más números naturales (1, 2, 3, 4, 5, …. 72, 73, 74, …etc) que números pares (2, 4, 6, 8, 10, 12,…etc). Usted… ¿qué contestaría? 

A priori, uno tiene la tentación (acertada en otro contexto), de contestar que hay más números naturales que pares, aunque más no sea, porque los pares forman una parte de todos los números. No son todos los números (porque faltan todos los impares), y es por eso que uno contestaría (con convicción): ¡no hay la misma cantidad! 

Sin embargo, reproduciendo el análisis que recién hicimos para las butacas del cine y las personas que están en la cola. En la respuesta que encontramos al final, usted habrá descubierto que no hace falta CONTAR. Basta con asignarle a cada butaca una persona y viceversa, pero esencialmente, el ‘acto’ o la ‘acción’ de ‘contar’, es innecesaria. 

Hagamos lo mismo entonces ahora con los números. Yo voy a proponerle esta asignación, algo así como si los números naturales fueran las personas que están esperando en la cola y los números pares, son las butacas del cine. Uno podría hacer así: al número uno, le asignamos el número dos. Al número dos, le asignamos el número cuatro. Al número tres, le asignamos el número seis…. Y así sigo: al número 53 le asignamos el número 106…. O más en general, al número n le asignamos el número….¡2n! 

Como usted advierte, a diferencia de lo que sucede cuando uno tiene una cantidad finita (ya sea por la cantidad de gente que está en la cola esperando para entrar o el número de butacas que hay dentro de un cine), en este caso, a cada número natural le corresponde un par y viceversa: ¡cada número par proviene de un número natural! Por ejemplo, si usted me preguntara qué número natural está asociado con el número 1.472, todo lo que hay que hacer es dividirlo por dos (cosa que siempre podremos hacer porque estos números son todos pares). El número 1.472 proviene entonces (o tiene asociado entonces), el número 736. 

Si seguimos con la misma idea que antes, todo natural tiene un par asociado y al revés, todo par, tiene un número natural asociado. Es decir: ni sobran butacas ni sobran personas en la cola, ni queda gente parada, ni nada…

Uno puede concluir, a pesar de cuán ‘anti-intuitivo’ parezca, que la cantidad de números naturales y números pares …¡es la misma! 

Justamente, esta situación se da únicamente cuando los conjuntos son infinitos, si no, no habría manera de llegar a esa instancia. En el mundo donde ‘viven’ los infinitos, en el mundo en donde ¡no se puede contar! , allí, es posible demostrar (como hicimos recién), que hay tantos pares como números. 

Más aún: ¿no le dan ganas de preguntarse –y después buscar la respuesta- si hay más números pares que impares? O si hay más números naturales que múltiplos de 5… o naturales que múltiplos de 7.

Y ya que seguimos avanzando: ¿habrá más números enteros (los que incluyen al número cero y a los números negativo), que números naturales. ¿Y si quiero ahora comparar si hay más números racionales  (los que en el colegio nos enseñaron como fracciones) que números naturales?...

Y cuando usted se haya convencido de lo que sucede, uno podría hacerse ahora una nueva pregunta: ¿todos los infinitos son iguales? ¿O es que hay infinitos que son más grandes que otros? 

¿No la/lo tientan todas estas preguntas? 

Inténtelo usted. No importa cuáles sean las conclusiones… siempre se pueden encontrar en un libro, o en internet, o preguntándolo… pero más allá de las respuestas … ¿no tiene ganas de pensar usted por su cuenta? 

Créame: vale la pena hacerlo y verá qué satisfacción produce descubrir este mundo nuevo, el mundo de los infinitos.