Quiero proponerle un problema para pensar. Mi idea es que usted se "entretenga" en soledad. Si no, quisiera que recorramos un camino conjunto y quiero mostrarle una forma de deducir la solución usando únicamente las herramientas que provee la lógica. Todo lo que usted tiene que aportar es ganas de pensar. Por supuesto, no hay una única forma de llegar a la respuesta, pero lo que me motiva a escribir este texto, es compartir la potencia que tiene el método deductivo, en donde cada paso tiene una explicación. Me explico.
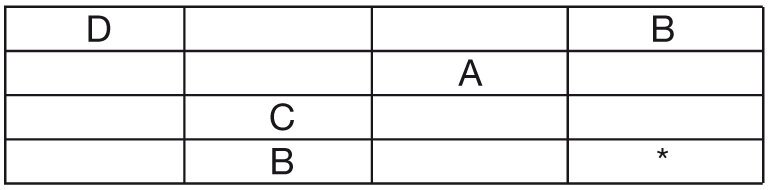
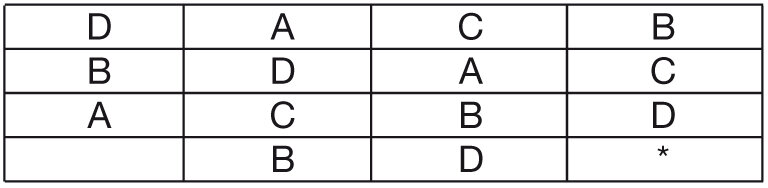
Fíjese en este tablero de 4 x 4.
Como usted ve, de las 16 casillas posibles, hay solamente cinco que están ocupadas. Usé las primeras cuatro letras del alfabeto: A,B,C y D.
El objetivo es completar el tablero de manera tal que en cada fila y en cada columna aparezca cada letra una sola vez.
Preguntas:
1) ¿Qué letra ocupa la casilla que tiene el asterisco?
2) ¿Hay una única solución?
Ahora, le toca a usted.
Una forma de pensar el problema
Este es el camino que elegí yo. Voy anotando cada uno de los pasos.
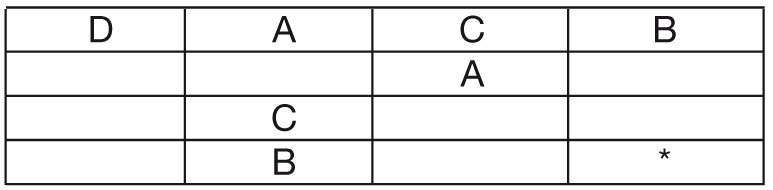
1) Mire la primera fila. Como ya están las letras D y B, tengo que decidir dónde poner la A y dónde poner la C. Como en la tercera columna ya hay una A, entonces eso fuerza a que allí vaya la C y por lo tanto, la letra A ocupa la primera fila y segunda columna. El tablero ahora queda así:
2) ¿Por dónde seguir? Si mira la segunda columna, falta llenar una sola casilla, y la única letra que falta es la D.
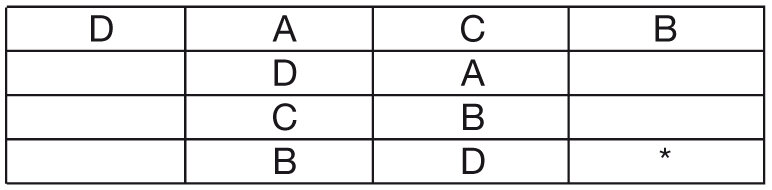
3) Ahora, fíjese en la tercera columna: faltan la B y la D. La B no puede ir en la última fila porque ya hay una B allí. Moraleja: la B va en la tercera fila (y tercera columna) y la D va en la cuarta fila. La grilla queda así:
¿No tiene ganas de seguir usted?
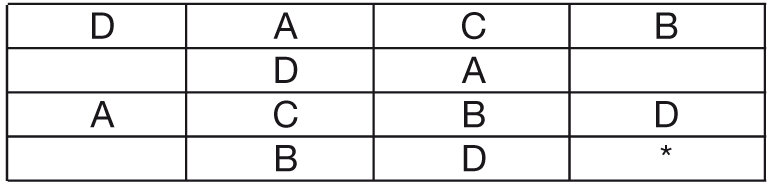
4) Ahora, mire la tercera fila: faltan la A y la D, pero como la D ya está en la primera fila, entonces la A va en la casilla en donde se cruzan la primera columna y la tercera fila y la D, en la última columna. Y queda así:
5) Falta poco. En la segunda fila, faltan la C y la B. La B no puede ir en la última columna, porque ya hay una B en la primera fila, por lo que la B va en la primera columna y la C va en la última. Se tiene esta última configuración:
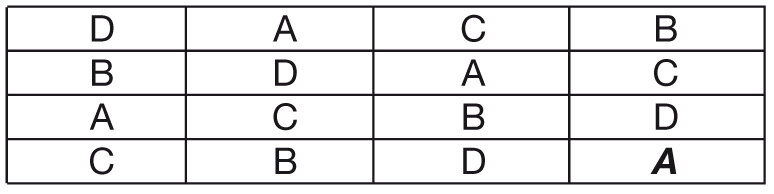
6) Para terminar: en la primera columna falta la C. Y listo: el asterisco se cubre con la letra A. Y eso contesta la pregunta.
Ahora, más allá del resultado final
¿qué otras conclusiones sacaría usted?
En principio, si usted me siguió cada uno de los pasos, advirtió que no había otra alternativa: cada paso fuerza los siguientes. No tuve que hacer ninguna elección entre varias posibilidades. Esto implica que ... ¡la solución es única! Es decir: no solo el problema tiene respuesta, sino que la que encontramos es la única posible. Y si me permite, debería haber escrito: la deducción que fuimos haciendo en cada etapa nos permitió construir la solución.
¿Por qué hice esto paso por paso? Porque esto es lo que uno suele hacer en la matemática cuando se enfrenta con situaciones de este tipo. Es como un árbol en donde uno va avanzando por cada rama, pero en cada bifurcación (o “multifurcación” si me permite inventar la palabra), la que termina eligiendo es la ¡única posible! Si cualquier otra persona empezara de otra forma, no podría llegar a otra respuesta porque la que encontramos entonces es la que fuerzan las circunstancias.
Y justamente de eso se trata: ¡una deducción!
