Hace diez años, Ernesto Tiffenberg me invitó a tomar un café en un bar en San Telmo, cerca de la redacción de Página/12. Allí fue cuando me propuso que escribiera algunas columnas para la contratapa, yo le dije: “¿Estás seguro? Mirá que yo escribo, por ejemplo, la demostración del Teorema de Pitágoras”. Ernesto no se inmutó. Y siguió: “Y yo te la publico”. Y así fue. El martes 31 de julio de 2007, en la contratapa del diario apareció la “tan mentada” demostración.(1)

¿Por qué recuerdo esta anécdota acá? Es que, ¿cuántas veces en su vida usted escuchó hablar del Teorema de Pitágo-ras? (2) ¿Cuántas veces realmente pensó en lo que decía? ¿Cuántas veces usó el teorema en su vida cotidiana? Me apuro a decir que es un teorema extraordinario, que tiene una utilidad asombrosa y que uno lo usa muchísimas más veces que las que se da cuenta, y lo hace “casi” en forma intuitiva, sin pensar necesariamente en lo que está haciendo. Pero eso dará lugar para una próxima nota.

Lo que quiero hacer acá es otra cosa. Acá quiero contar un problema que se le ocurrió a un joven español. Su nombre es Iñigo Tena Núñez y lo notable es que ¡no es matemático! Pero Iñigo tiene un blog cuyo objetivo es desarrollar la capacidad para pensar y es por eso que Pablo Coll (3) me lo propuso con la idea de que lo usáramos en uno de los episodios de Alterados por Pi (año 2014), y más allá de haberlo desarrollado en una escuela pública de la Argentina, me interesa publicarlo también en Página/12.

Eso sí: no se deje intimidar por las palabras “teorema”, “Pitágoras”, “demostración”, “catetos”, “hipotenusa”, etc. ¿Puedo pedirle que apele a su capacidad para pensar? Verá que cuando le dedique un rato, resuelva el problema o no, se sentirá mejor. Habrá descubierto que algo que “supo” toda la vida, en realidad le sirvió para contestar una pregunta que de otra forma hubiera sido muchísimo más complicado encontrar la respuesta. No digo que no se pueda (seguro que sí), pero verá que con las herramientas que tiene, está en condiciones de avanzar en una dirección que nunca había imaginado.

Ahora sí, acá voy. Suponga que usted mira la figura 1:

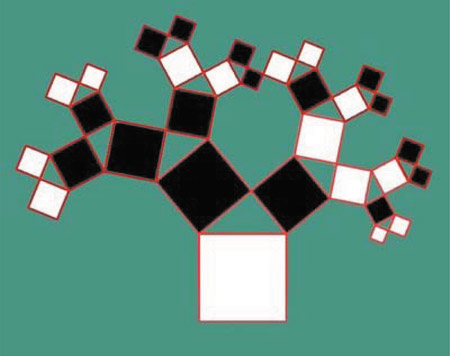
Fíjese en las áreas “pintadas de negro” y las que están “pintadas de blanco”.

Si uno las sumara imaginariamente... ¿cuál le parece que es más grande?

Eso es todo. Todo lo que hace falta contestar es cuál de las dos áreas es la más grande de las dos. Y lo único que le sugiero es que no lea lo que sigue sin haberle dedicado al menos un rato en pensar el problema.

Idea para encontrar la solución

A esta altura, usted debe haber imaginado que si hice toda la introducción sobre el Teorema de Pitágoras es porque en alguna parte habría de aparecer. Y así es: fíjese en el cuadrado mayor, el de área blanca que está apoyado sobre la base. Quiero tomar ese cuadrado como referencia.

En la tapa de arriba de ese cuadrado, hay dibujado un triángulo. Si usted le presta atención a ese rectángulo verá que es “rectángulo”, o sea, tiene un ángulo de 90 grados o ángulo “recto”. En principio no parece porque la hipotenusa coincide con la tapa de ese cuadrado, pero ni bien uno le presta un poco más de atención, descubre que sí, que es un triángulo rectángulo.

Ahora bien, el Teorema de Pitágoras dice –justamente– que “en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. ¿Cómo usar esta afirmación en este caso?

Lo que uno deduce entonces es que el cuadrado blanco (el que estoy considerando como referencia) tiene área igual a la “suma de los cuadrados de los catetos”. Y esos cuadrados están representados por los cuadrados pintados de negro. ¿Alguna vez pensó esto? Cuando Pitágoras hacía referencia a los “cuadrados” de los catetos o el “cuadrado” de la hipotenusa, uno puede pensar que justamente son los cuadrados que uno podría dibujar en donde cada lado corresponde o bien a uno de los catetos o bien a la hipotenusa.

En resumen, el teorema dice que el área del cuadrado blanco es igual a la suma de las áreas de los dos cuadrados negros. Por lo tanto, cuando yo quiera evaluar cuál área es más grande (la que aparece pintada de negro o la que aparece pintada de blanco), esas tres áreas se compensan (son iguales).

Con esa misma idea, le propongo ahora que “recorra” las otras figuras, buscando triángulos rectángulos y áreas negras y blancas. Fíjese en qué casos puede hacer que se cancelen o en cuales hay más de un color que de otro.

Al finalizar el recorrido, se encontrará con la figura 2. Yo fui “encapsulando” las áreas blancas y negras que se compensan. Lo que no pude hacer es “encerrar” a los tres cuadrados que tienen áreas negras y el único cuadrado blanco cuya área no pude equiparar con otras.

¿Qué se puede deducir? De los tres cuadrados negros que no pude encerrar, tienen la particularidad que los dos más pequeños tienen área igual al área del cuadrado negro más grande (por Pitágoras otra vez). Por otro lado, el cuadrado blanco tiene área igual a uno de esos cuadrados negros más uno que debería ser de área más pequeña.

Moraleja: el área negra es mayor que el área blanca, que es lo que queríamos dilucidar. ¿No le parece notable?

1) http://www.pagina12.com.ar/diario/contratapa/138892820070731.html
2) “En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.”
3) Amigo y doctor en Ciencias de la Computación, egresado de la UBA y uno de los más prolíficos “contenidistas” de Alterados por Pi.i.