A veces, las más complejas investigaciones matemáticas se centran en las más simples de las cuestiones. Simples, en apariencia. Y si no, que le pregunten al matemático australiano Burkard Polster, de la Universidad de Monash (Australia), que, para encontrar un enigma a resolver, no tuvo que ver más allá de sus zapatos: el curioso científico reveló matemáticamente la mejor manera de atarse el calzado con mayor fuerza y la menor extensión de cordón posible. Un trabajo que los malignos jurados del Ig Nobel (ver Futuro 16/11) podrían llegar a considerar.
“El problema puede parecer simple, pero no lo es en absoluto”, afirmó Polster a Futuro. “Sólo para dar una idea de su complejidad, con 6 pares de agujeros hay 43.200 maneras diferentes de atar un zapato; con 7, 400 millones”.
Lo primero que hizo el matemático australiano fue identificar las variables: número de agujeros del zapato (2n), la distancia entre ellos (h) y la longitud del cordón (k). Y luego las combinó en una ecuación matemática. El resultado: las hasta ahora más populares maneras de atarse los zapatos, en forma cruzada y la invertida (con un cordón de un extremo al otro), son las más fuertes. Pero, según Polster, ninguna de las dos son totalmente eficientes. 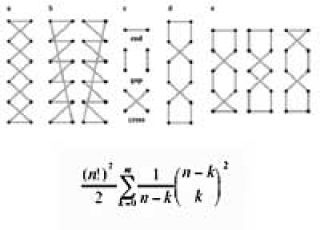En cambio, la que sí lo sería, al menos matemáticamente, es la poco conocida bow-tie (nudo en forma de moño o nudo mariposa, ver imagen) que tiene la peculiaridad de utilizar mucho menos cordón que las otras. Consiste en pasar el cordón por los agujeros de una misma columna para luego cruzarlos con los ojales opuestos.

Una historia enlazada
Según cuentan los historiadores, los cordones no son precisamente algo muy nuevo: hay murales en el palacio de Nínive (del 650 a.C.) que muestran a un rey asirio con sandalias amarradas con elaborados nudos. En la era moderna, los primeros zapatos con cordones en vez de hebillas fueron los famosos “oxfords”, llamados así luego de que un grupo de estudiantes de la Universidad de Oxford (Inglaterra) los hiciese populares en 1640.
Durante la Revolución Francesa, en 1789, las tradicionales hebillas eran consideradas “aristocráticas” mientras que los cordones, “democráticos”. Aun así, esta nueva tendencia en el calzado tuvo su lado negativo. Su masiva introducción en el Reino Unido, por ejemplo, produjo más de 20 mil despidos en Birmingham, principal centro de la industria de las hebillas. Del otro lado del Atlántico, Thomas Jefferson, el tercer presidente de Estados Unidos (1801-1809) fue una de las primeras figuras políticas prominentes en usar zapatos con cordones.

Ecuaciones y poleas
Para llegar a estos notables resultados, publicados nada menos que en la revista Nature, Polster usó métodos matemáticos de optimización combinatoria en un zapato imaginariocuyos agujeros están perfectamente alineados y en un mismo plano. También ignoró ciertas propiedades físicas como la fricción ejercida por el cordón en el ojal y los materiales utilizados en su confección.
Luego, para determinar las formas más fuertes de atarse los zapatos, Polster consideró que los cordones, una vez estirados, actúan como un sistema de poleas en los que las columnas de los agujeros se atraen y mantienen firme al pie, generando una tensión a lo largo del cordón. La fuerza del sistema de atado depende de la distancia entre ambas columnas. Cuando los ojales están relativamente separados pero el espacio entre ambas columnas es corto, la forma cruzada es la más fuerte. No pasa lo mismo si la distancia horizontal que separa a las columnas es mayor. En ese caso, la forma invertida es la ideal.
En realidad, este divertimento matemático, no casualmente, limita con la optimización combinatoria, en la que se abordan problemas en apariencia triviales, pero de solución complejísima, como el “problema del viajante de comercio”, o el “problema del visitante del museo”.
“Para mí todo esto fue sólo un problema para pensar en mi tiempo libre”, explicó Polster, nuevamente, a Futuro. “Sin duda, para relajarme de la matemática seria, nada mejor que matemática divertida.” Parece que el tiempo de diversión del científico australiano aún no termina. Su próximo proyecto de investigación lo demuestra: la matemática del origami.