Lo que sigue es pura matemática. Parece disfrazada de juego de damas o de soldados, pero no le crea: es una manera más de hacer matemática.

Esta presentación tiene que ver con la percepción que existe de la matemática en el mundo. Al leer lo que figura más abajo, verá que usted empieza a dudar también. Es decir, va a creer que estoy exagerando, porque lo que sigue se va parecer mucho a un “juego” con el que uno podría entretenerse cualquier noche jugando con amigos o bien a las “damas” o cualquier juego que requiera usar un tablero (ajedrez, ludo, etc). Intuyo que más o menos todos hemos estado involucrados en alguno de ellos alguna vez en nuestras vidas.

Bueno, créame: no exagero. Por supuesto, no digo que sea (ni mucho menos) lo único que hay o habría que enseñar de matemática, pero si uno mostrara en los colegios y escuelas que “hacer matemática” es también pensar soluciones de juegos del tipo que figuran más abajo, y/o diseñar estrategias para ver si un problema tiene solución, apuesto a que los jóvenes (a quienes no culpo de ninguna forma), que hoy detestan esta materia o que no saben cómo hacer para zafar de las horas de matemática que tienen que cursar inexorablemente), tendrían todos (o casi todos) un interés distinto.

Por otro lado, ¿a quién no le gusta jugar? ¿Quién no jugó alguna vez a algo? ¿Por qué el jugar y el pensar, o el disfrutar con la mezcla de ambos, no forma parte de nuestros programas de matemática en las etapas de formación?

El problema que sigue no sólo no es mío sino que está muy lejos de que alguien pueda apropiárselo. Le pertenece al excelente matemático inglés John Conway (que ya fue presentado en este mismo diario, Página/12, el 24 de julio de 2006, página 40) y se lo conoce en el mundo bajo el nombre de “Los Soldados de Conway”.

Si bien no hace falta para entender el planteo del problema es útil haber jugado alguna vez a las damas, simplemente porque ésa es la forma en la que uno avanza con sus piezas, saltando por encima de otras. Pero no se preocupe si usted nunca jugó porque no le acarrea ninguna desventaja.

Lo que Conway propuso fue lo siguiente: imagine que tiene un tablero de ajedrez, pero infinito. Cuando escribo la palabra infinito es porque estoy pensando que en lugar de ser un tablero común de 8 x 8, éste se extiende indefinidamente hacia derecha e izquierda, y también hacia arriba y abajo.

En lugar de tener 16 piezas como en el juego de damas, usted tiene a su disposición la cantidad de piezas que quiera. Justamente Conway llama “soldados” a estas fichas y de ahí el nombre del juego.

Ahora, haga de cuenta de que hay una línea divisoria horizontal que separa el tablero en dos: la parte de “arriba” y la de “abajo”.

En la parte de “arriba” no hay ningún soldado. Está todo vacío. En cambio, en la parte de “abajo” usted puede usar las piezas que quiera. Para poder “avanzar” en el tablero (como en las damas) se trata de “saltar” por encima de una ficha en forma horizontal o vertical, siempre y cuando uno “aterrice” en un lugar vacío.

¿Cuál es el objetivo del juego? Avanzar hacia arriba (con movimientos “legales”) de manera tal de poder ubicar un soldado lo más “arriba” posible. Es decir, tratar de ocupar alguna casilla en alguna fila de las que están “arriba” de la línea divisoria, y que ese casillero esté ubicado lo más arriba que se pueda.

Empiezo con algunas preguntas: ¿se le ocurre alguna forma de llegar a la “primera” fila de arriba? (la/lo dejo a usted para que piense y luego sigo yo).

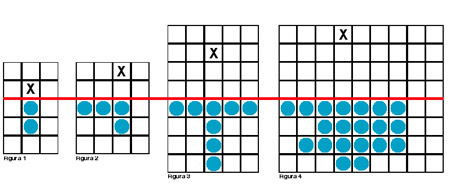
Como se ve en la figura 1, la solución es muy sencilla. Basta con disponer los soldados como se ve allí, y entonces uno alcanza la primera fila inmediatamente. Y lo más importante es que lo pudo hacer usando solamente dos soldados y un solo movimiento.

Ahora, Conway dobla la apuesta. ¿Hay alguna forma de distribuir sus piezas del lado de abajo de manera tal de llegar (usando los movimientos permitidos) a la “segunda” fila de arriba?

La respuesta es que sí, que se puede. Descubra usted, entonces, cuántos soldados (piezas) le hicieron falta y cuántos movimientos usó. Vea la figura 2.

Observe que ahora son necesarias cuatro piezas y tres pasos con esa distribución. Vale la pena que usted se detenga un rato y piense por qué no se puede hacer en un número menor de pasos.

Es que seguro que hace falta más de un paso, porque con uno solo no se puede llegar a la segunda fila, porque haría falta que hubiera un soldado en la primera, y como al principio del juego no hay nada del “lado de arriba”, inexorablemente hemos necesitado un paso antes para poner esa ficha allí. Luego, un paso no es suficiente.

Después, debajo de la pieza que quedó arriba en la primera fila, no puede haber quedado ninguna porque uno usó ese casillero para poder llevar esa pieza hacia arriba. Luego, hace falta un movimiento más para poner otra vez una pieza en ese lugar (para que ésta pueda “comer” a la que está arriba y de esa forma depositar la que queremos en la segunda fila)

En resumen, uno lo puede hacer pero necesita cuatro piezas y tres pasos.

¿Y si uno quiere llegar a la tercera fila? ¿O a la cuarta o quinta? ¿Y más arriba? ¿Cuántos soldados hacen falta? ¿Y cuántos pasos?

Lo interesante es lo siguiente: para poder llegar a la tercera fila, hacen falta ocho piezas distribuidas como se ve en la figura 3. Y para llegar a la cuarta fila son necesarias 20 (veinte) piezas y una de las distribuciones que se pueden usar es la que se ve en la figura 4.

Pero ahora, uno tropieza con una dificultad. Intente usted llegar hasta la quinta fila y fíjese cuánta suerte tiene. Créame: trate de llegar hasta allí arriba y verá lo que pasa.

Lo que sucede es que hubo mucha gente tratando de encontrar alguna forma de llegar a la quinta fila de “arriba” pero, como le pasó a usted, no podían llegar. No importaba la forma que eligieran, ni la distribución de las piezas... no lo podían lograr (y por eso le propuse que intentara usted, para poder comprender el grado de dificultad).

Hasta que John Conway probó que, no importa con cuántas piezas empiece ni cuantos pasos dé, ¡no hay manera de llegar a la quinta fila! La demostración (*) escapa a lo que yo puedo hacer acá, pero créame que lo que hace Conway es usar un poco de matemática (no muy avanzada) y mucha creatividad. Y eso es lo que (creo) deberíamos aprender a valorar más: la creatividad, y no tanto el conocimiento enciclopédico. Importa más estimularnos a pensar distinto, por fuera de lo convencional. Por lo tanto, más allá de encontrar la solución, lo notable es que se pueda demostrar que independientemente de lo que usted haga, no va a poder llegar hasta allí arriba.

Eso es lo que impacta. Eso es lo que transforma este juego (y no tendría nada de malo que solamente fuera un juego) en algo tan valioso. La posibilidad de pensar cómo avanzar sin saber si uno va a poder o no llegar a destino. Uno puede presumir que es uno el que no encuentra la fórmula para hacerlo, pero que otro podría llegar si hiciera algo diferente que a usted no se le ocurre.

Por eso, lo extraordinario es que haya alguien (Conway) que demostró que no dependía de usted, sino que nadie va a poder.

De eso se trata. De poder disfrutar de pensar aun sabiendo que el problema que uno encara podría no tener solución. El hecho de poder demostrar que el problema no tiene solución es un avance increíble en la mayoría de las situaciones de la vida que uno enfrenta. Y, por eso, la matemática tiene semejante potencia.

* La demostración de que no se puede llegar hasta la quinta fila se puede encontrar (en inglés) en: http://plus.maths.org/issue12/xfile/