[cerrar]

Comparta esta nota con un amigo

E-Mail de su amigo
Su nombre
Su E-Mail

Por Leonardo Moledo

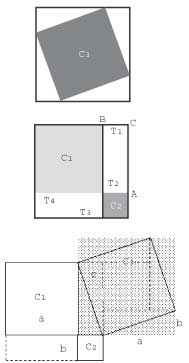
–A todo el mundo le encantó la demostración china del teorema de Pitágoras –dijo el Comisario Inspector– hubo unanimidad absoluta entre los lectores.
–Es que, verdaderamente, es muy elegante –dijo Kuhn.
–Y además, ninguno de los lectores encontró ningún error, aunque uno de ellos sugirió que era una verificación y no una demostración.

Desde luego, yo creo que es una demostración, aunque hay un paso lógico que me falta, y es el siguiente. ¿Cómo se sabe que los triángulos de la segunda figura son iguales a los de la primera?
–Daniel Rosenvasser lo explica con un dibujo –dijo Kuhn.

–Bueno –dijo el Comisario Inspector–. No tuve tiempo de analizarlo, pero ¿cómo se sabe que los dos cuadrados grandes son iguales? Daniel Rosenvasser dice que es evidente. A mí no me resulta tan evidente, pero lo pensaré mejor.
–Enigma –alertó Kuhn.
–Bueno –dijo el Comisario Inspector–. El enigma de hoy me lo envió Tito Weissmann hace un tiempo ya, y dice así:
“Hay tres cajas cerradas y cada una contiene dos bolillas. Una caja contiene dos bolillas negras, otra dos blancas, y otra una negra y una blanca. Las cajas están etiquetadas: NN, BB, BN, pero resulta que las etiquetas han sido cambiadas y ninguna está en su lugar”.
–¿Y cuál es el enigma? –preguntó Kuhn.
–El siguiente: ¿cuál es el número mínimo de bolillas que tengo que sacar para saber qué contiene exactamente cada caja?

¿Qué piensan nuestros lectores? ¿Tiene razón Daniel Rosenvasser? ¿Y cuántas bolillas hay que sacar?

Correo de lectores

CORRECCION
Mi respuesta al problema al problema de las monedas de Rutherford que se publicó el otro día era correcta pero se deslizó un involuntario error en los cálculos. Si la bolsa que contiene las monedas falsas fuese la primera, al éstas pesar 0,9 gramos, el peso total sería de 5049,9 gramos (y no 5049 como indiqué suponiendo una diferencia de 1 gramo en lugar de 0,1 gramos); si fuese la segunda sería de 5049,8 gramos ... si fuese la centésima 5040 gramos. La solución ofrecida por Edgar Anzil (repartir la 100 bolsas en cantidades iguales en los dos platos de una balanza e ir retirando de cada plato hasta que queden balanceadas) no es correcta por dos razones: a) porque implicaría más de una pesada y b) porque supone que todas las bolsas contienen el mismo número de monedas.
Marcelo Leonardo Levinas